|
||||||
| Applied
Econometrics
Econ 508 - Fall 2008 e-Tutorial 3: Box-Cox Transformation and Partial Residual Plot |
||||||
| Welcome
to the third issue of e-Tutorial, the on-line
help to Econ 508. The introductory material presented below is designed
to enhance your understanding of the topics and your performance on the
homework. This issue focuses on the basic features of Box-Cox transformations
and Partial Residual Plots.
Introduction: In the problem set 1, question 1, you are asked to estimate two demand equations for bread using the data set available here (or if you prefer, visit the data set collection at the Econ 508 web page, under the name "giffen"). Save the data using the techniques suggested on e-Tutorial1 and 2. As a general guideline, I suggest you to open a log file to keep track of all econometric experiments you are going to perform. Parts (i)-(iii)
involve simple linear regression and hypothesis testing that should be
straightforward to solve once you familiarize with the software you adopted.
For every hypothesis testing, please make clear what are the null and alternative
hypotheses. Please also provide a simple table with the main estimation
results. I recommend you to ALWAYS include standard deviations for ALL
parameters you estimate. Another useful advice is to summarize your main
conclusions ("bullets" are a good way to express them on the homework).
Finally, graphs are very welcome as long as you provide labels and refer
to them on your comments. Don't include any remaining material (e.g., software
output or your preliminary regressions) in your report.
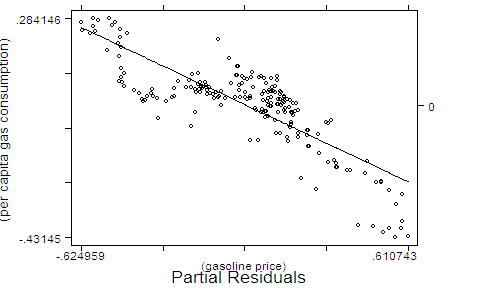
Partial Residual Plot: Question 1, part (iv) requires you to compare the plots of the Engel curves for bread in the "short" and "long" versions of the model using partial residual plot for the latter model. As mentioned in Professor Koenker's Lecture 2, "the partial residual plot is a device for representing the final step of a multivariate regression result as a bivariate scatterplot." Here is how you do that: * Theorem: (Gauss-Frisch-Waugh): Recall the results of the Gauss-Frisch-Waugh theorem in Professor Koenker's Lecture Note 2 (pages 8-9). Here you will see that you can obtain the same coefficient and standard deviation for a given covariate by using partial residual regression. I will show the result using the gasoline demand data available here. In this data set, Y corresponds to the per capita gas consumption, P is the gas price, and Z is the per capita income. The variables are already in the logarithmic form, so that we are actually estimating log-linear models. At first you run the full model (Model A) and observe the coefficient and standard deviation of P. Then you run a shorter version of the model (Model B), excluding P. You get the residuals of this partial regression and call them "resB". After that you run another short model (Model C), but in this case you regress the omitted variable P on the same covariates of model B. You obtain the residuals of the latter model and call them "resC". Finally, you regress the residuals of the model B on the residuals of the model C. The algorithm for the exercise is as follows: Model A:
regress Y P Z
And the econometric output is as follows: . gen Y=lny . gen P=lnp . gen Z=lnz . *Model A: Y = \alpha_{0} + \alpha_{1}*P + \alpha_{2}*Z
. regress Y P Z
Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 2, 198) = 1674.11 Model | 21.0866833 2 10.5433417 Prob > F = 0.0000 Residual | 1.24698236 198 .006297891 R-squared = 0.9442 ---------+------------------------------ Adj R-squared = 0.9436 Total | 22.3336657 200 .111668328 Root MSE = .07936 ------------------------------------------------------------------------------ Y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- P | -.4075322 .0196435 -20.746 0.000 -.4462696 -.3687948 Z | 1.75935 .0419446 41.945 0.000 1.676634 1.842065 _cons | -5.266504 .1121704 -46.951 0.000 -5.487706 -5.045303 ------------------------------------------------------------------------------ . *Model B: Y = \beta_{0} + \beta_{1}*Z
. regress Y Z
Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 1, 199) = 923.98 Model | 18.3759978 1 18.3759978 Prob > F = 0.0000 Residual | 3.95766793 199 .019887779 R-squared = 0.8228 ---------+------------------------------ Adj R-squared = 0.8219 Total | 22.3336657 200 .111668328 Root MSE = .14102 ------------------------------------------------------------------------------ Y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- Z | .9735875 .0320289 30.397 0.000 .9104278 1.036747 _cons | -3.106386 .0741504 -41.893 0.000 -3.252608 -2.960165 ------------------------------------------------------------------------------ . *Residuals from Model B: . predict resB, resid . *Model C: P = \gamma_{0} + \gamma_{1}*Z
. regress P Z
Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 1, 199) = 878.73 Model | 72.0708177 1 72.0708177 Prob > F = 0.0000 Residual | 16.321319 199 .082016678 R-squared = 0.8154 ---------+------------------------------ Adj R-squared = 0.8144 Total | 88.3921367 200 .441960684 Root MSE = .28639 ------------------------------------------------------------------------------ P | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- Z | 1.928099 .065043 29.643 0.000 1.799837 2.056361 _cons | -5.300484 .1505815 -35.200 0.000 -5.597424 -5.003544 ------------------------------------------------------------------------------ . *Residuals from Model C: . predict resC, resid . *Gauss-Frisch-Waugh regression: resB = \theta_{0} + \theta_{1}*resC
. regress resB resC
Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 1, 199) = 432.59 Model | 2.71068559 1 2.71068559 Prob > F = 0.0000 Residual | 1.24698237 199 .006266243 R-squared = 0.6849 ---------+------------------------------ Adj R-squared = 0.6833 Total | 3.95766796 200 .01978834 Root MSE = .07916 ------------------------------------------------------------------------------ resB | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- resC | -.4075322 .0195941 -20.799 0.000 -.446171 -.3688934 _cons | -5.37e-10 .0055835 0.000 1.000 -.0110104 .0110104 ------------------------------------------------------------------------------ . *Now we can plot those resB vs. resC, and insert a fitting line: . predict gfw (option xb assumed; fitted values) . graph resB gfw resC, title(Partial Residuals) rlab(0) c(.l) s(oi) l1((per ca > pita gas consumption)) b2((gasoline price)) sort .
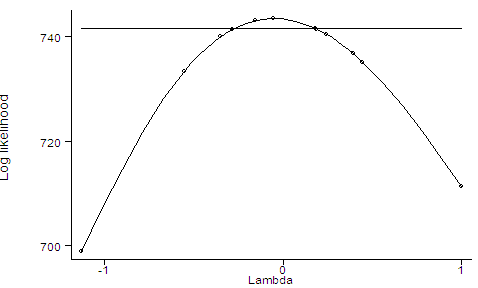
For question 2, parts (a)-(d) are also straightforward to be done. You are expected to calculate the estimates in both linear and log-linear form. Besides them, you are expected to run a Box-Cox version of the model, and interpret it. Here I will give you some help by using the same gasoline demand data as above (click here to download it, if you haven't done yet). Just for a minute, suppose somebody told you that a nice gasoline demand equation should also include two additional covariates: the squared price of gas, and the effect of price times income. You can obtain those variables as follows: . gen Psq=P^2 . gen PZ=P*ZNext you are asked to run this extended model, in a traditional log-linear form (remember that all covariates are already in logs). So, the easiest way to do that is as follows: . regress Y P Z Psq PZ Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 4, 196) = 1499.50 Model | 21.6269476 4 5.4067369 Prob > F = 0.0000 Residual | .706718113 196 .003605705 R-squared = 0.9684 ---------+------------------------------ Adj R-squared = 0.9677 Total | 22.3336657 200 .111668328 Root MSE = .06005 ------------------------------------------------------------------------------ Y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- P | -2.573682 .1858084 -13.851 0.000 -2.940122 -2.207242 Z | 2.571179 .077643 33.115 0.000 2.418056 2.724302 Psq | -.2712707 .0375378 -7.227 0.000 -.3453005 -.1972408 PZ | .7170179 .0593085 12.090 0.000 .6000533 .8339826 _cons | -7.391471 .2032132 -36.373 0.000 -7.792236 -6.990706 ------------------------------------------------------------------------------The log-linear form seems to be a nice attempt to estimate the gasoline demand. Next, suppose you are so confident on this model that you write a paper about the topic and send it to a journal. Two weeks later you receive a letter from a referee saying she is suspicious about your log-linear equation. She asks you to reestimate the same model but using the dependent variable linearly (i.e., without the logs), and the rest of the equation remaining as before. She asks you to revise and resubmit the paper with your new findings. In the search for elements that support your original model, you start the following experiment: (i) run the model suggested by the referee, using a Box-Cox transformation to find the MLE of \lambda, (ii) plot the concentrated log-likelihood function, and (iii) reestimate the model conditional on the MLE of \lambda: . gen y=exp(Y) . boxcox y P Z Psq PZ, level (95) graph (note: iterations performed using zero =.001) Iteration Lambda Zero Variance LL ------------------------------------------------------------ 0 1.0000 -51.95892 .000848119 710.78526 1 -1.1304 77.09366 .000947193 699.68173 2 0.3930 -29.04524 .000657527 736.36598 3 -0.1569 7.78408 .000615281 743.03987 4 -0.0569 0.12662 .000613114 743.39446 5 -0.0553 -0.00025 .000613117 743.39394 ------------------------------------------------------------ Iterations for lower confidence interval: Iteration Lambda Zero Variance LL ------------------------------------------------------------ 0 -0.5553 -8.08405 .000677294 733.38916 1 -0.3504 -1.57634 .000634827 739.89687 2 -0.2824 -0.15841 .000625933 741.31480 3 -0.2734 0.00038 .000624945 741.47359 ------------------------------------------------------------ Iterations for upper confidence interval: Iteration Lambda Zero Variance LL ------------------------------------------------------------ 0 0.4447 6.37510 .000665875 735.09811 1 0.2437 1.14562 .000632112 740.32759 2 0.1879 0.11467 .000625661 741.35854 3 0.1811 0.00364 .00062497 741.46957 4 0.1809 0.00007 .000624948 741.47314 ------------------------------------------------------------ Transform: (y^L-1)/L L [95% Conf. Interval] Log Likelihood ---------------------------------------------------- -0.0553 -0.2734 0.1809 743.39394 Test: L == -1 chi2(1) = 69.69 Pr>chi2 = 0.0000 L == 0 chi2(1) = 0.19 Pr>chi2 = 0.6662 L == 1 chi2(1) = 64.18 Pr>chi2 = 0.0000 (type regress without arguments for regression estimates conditional on L) . regress Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 4, 196) = 1508.12 Model | 23.9317812 4 5.9829453 Prob > F = 0.0000 Residual | .777562769 196 .003967157 R-squared = 0.9685 ---------+------------------------------ Adj R-squared = 0.9679 Total | 24.709344 200 .12354672 Root MSE = .06299 ------------------------------------------------------------------------------ _boxcox | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- P | -2.630026 .1948992 -13.494 0.000 -3.014395 -2.245657 Z | 2.667722 .0814417 32.756 0.000 2.507108 2.828337 Psq | -.2810604 .0393744 -7.138 0.000 -.3587123 -.2034086 PZ | .7261529 .0622102 11.673 0.000 .6034657 .8488401 _cons | -7.658475 .2131554 -35.929 0.000 -8.078848 -7.238102 ------------------------------------------------------------------------------As you see, the MLE for \lambda is very close to zero. The picture is drawn using smoothing spline techniques to help you envisage the log-likelihood function and the MLE of \lambda. The horizontal line corresponds to the 95% confidence interval. The latter regression (conditional on the MLE of \lambda) provides results close to your log-linear suggestion. Now you have reasonable support to write back the referee and defend your original model. Andrews Test: Finally, for the Econ 508 problem set 1, question 2, you are also required to perform the David Andrews (1971) test. As an example, I use the same gasoline data as above, and follow the routine on Professor Koenker's Lecture Note 2: (i) Run the linear model and get the predicted values of y (call this variable yhat): . gen p=exp(P) . gen z=exp(Z) . regress y p z Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 2, 198) = 1609.94 Model | 3.70695117 2 1.85347559 Prob > F = 0.0000 Residual | .227951976 198 .001151273 R-squared = 0.9421 ---------+------------------------------ Adj R-squared = 0.9415 Total | 3.93490315 200 .019674516 Root MSE = .03393 ------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- p | -.3375906 .0144982 -23.285 0.000 -.3661814 -.3089999 z | .0741067 .0016292 45.487 0.000 .0708939 .0773195 _cons | -.1536729 .0112284 -13.686 0.000 -.1758155 -.1315303 ------------------------------------------------------------------------------ . predict yhat (option xb assumed; fitted values)
. gen LY=log(yhat) . gen YLY=yhat*LY . regress y p z YLY Source | SS df MS Number of obs = 201 ---------+------------------------------ F( 3, 197) = 1610.62 Model | 3.78075786 3 1.26025262 Prob > F = 0.0000 Residual | .15414529 197 .000782463 R-squared = 0.9608 ---------+------------------------------ Adj R-squared = 0.9602 Total | 3.93490315 200 .019674516 Root MSE = .02797 ------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- p | -.2958436 .0127019 -23.291 0.000 -.3208928 -.2707945 z | .0651617 .0016286 40.012 0.000 .0619501 .0683734 YLY | 1.082626 .1114711 9.712 0.000 .8627956 1.302455 _cons | .2845145 .0460572 6.177 0.000 .1936861 .375343 ------------------------------------------------------------------------------ . test YLY ( 1) YLY = 0.0 F( 1, 197) = 94.33 Prob > F = 0.0000From the test above we can reject the null hypothesis that \gamma =0. Can you interpret what does this mean? Using
R:
|
||||||