Question 1:

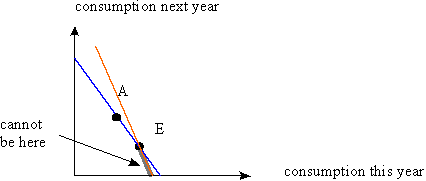
• The present value of his endowment is 2,000+1,100/(1+r)=3,000 because r=0.1.
• His marginal rate of substitution is MRS=-c₂/c₁.
• The equation of the budget line in future value form is (1+r)c₁+c₂=2,000(1+r)+1,100. In present value form it is given by c₁+c₂/(1+r)=2,000+1,100/(1+r)=3,000. Thus, the slope of the budget line is -(1+r)=-1.1. Thus, we get -c₂/c₁=-1.1 and c₁+c₂/(1.1)=3,000.
• The solution is given by c₁=1,500 and c₂=1,650.
• His endowment in period 1 is 2,000. Thus, he saves 2,000-1,500=500.
  

• If r=20, then (1+r)c₁+c₂=2,000(1+r)+1,100 implies 1.2c₁+c₂=2,400+1,100=3,500. The slope of the budget line is -1.2. Thus, -c₂/c₁=-1.2. This implies c₁=1458.333 and c₂=1,750.
• He now saves 2,000-1458,333=541.666.

Question 2:

• Note that the budget set with the red budget line (this is the budget line corresponding to the case where he invests in the first project) contains the original budget set (denoted by the blue line). Thus, since the budget set is strictly larger, he is better off investing in the project.
  

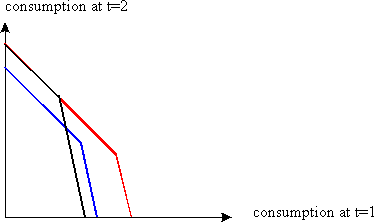
• The budget set corresponding to the second project (black budget line) does not contain the original budget set any more. Neither does the original budget set contain this alternative one. Thus, in each of the two budget sets, there are some consumption bundles which are not in the other budget. Therefore without knowing the agent's preferences we cannot tell whether or not he is better off.

Question 3:

• (a) If the system is not approved, then the Condor has a loss of 5 Dollars per share, because the price drops from 10 Dollars to 5 Dollars per share. Thus, he looses 5x Dollars. Therefore c_NA=50,000-5x.
• (b) We know that c_A=50,000+5x and c_NA=50,000-5x. Adding the two equations yields c_A+c_NA=100,000. Thus, 0.5c_A+0.5c_NA=50,000.
• (c) Condor's MRS is given by MRS(c_A,c_NA)=-3c_NA/c_A. At the optimal consumption choice, the MRS must be equal to the slope of the budget line. Thus, -3c_NA/c_A=-1 which implies c_A/c_NA=3.
• (d) The last equation is equivalent to 3c_NA=c_A. Inserting this in the budget line equation yields c_NA=75,000 and c_NA=25,000. Now recall that c_A=50,000+5x and c_NA=50,000-5x. Inserting c_NA=75,000 or c_NA=25,000 into the appropriate equation yields x=5,000, i.e., Condor will buy 5,000 shares.

Question 4:

• (a) If he wins the bet, he will have 120 Dollars. If he looses, he will have 80 Dollars. His expected utility from taking the bet is 0.25u(120)+0.75u(80), where u(x)=x² is the von Neumann Morgenstern utility function. Because u(120)=14,400 and u(80)=6400, the expected utility is 8,400. In contrast, if he does not take the bet he has 100 Dollars with probability 1. Thus, his ``expected'' utility is u(100)=10,000. Thus, he will not accep this bet.
• (b) No he will have 200 Dollars if he wins, and 0 Dollars if he looses. His expected utility from taking the bet is therefore 0.25u(200)+0.75u(0)=10,000. Thus, he is exactly indifferent between taking the bet and not taking the bet.
• (c) His preferences are described by u(c₁,c₂)=0.25c₁²+0.75c₂², because the probability of event 1 is 0.25 and the probability of event 2 is 0.75. Thus, u(100,100)=2,500+7,500=10,000. The indifference curve through (100,100) is therefore given by the equation
  0.25c₁²+0.75c₂²=10,000.

  For example, if c₁=0 then 0.75c₂²=10,000. Hence c₂²=13,333. Thus, c₂=115. Similarly, if c₂=0 then 0.25c₁²=10,000. Hence c₁²=40,000. Thus, c₁=200. The indifference curve is the blue curve in the graph.

  

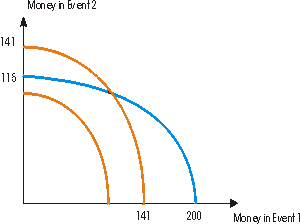
• (d) Now his preferences are described by u(c₁,c₂)=0.5c₁²+0.5c₂², because the probability of each event 0.5. Again, u(100,100)=10,000. Thus, the indifference curve is given by 0.5c₁²+0.5c₂²=10,000. For example, if c₁=0 then 0.5c₂²=10,000. Hence, c₂²=20,000, which implies c₂=141. Similarly, if c₂=0 then then c₁=141. Two indifference curves are drawn as red curves in the graph.

Question 5:

• The expected utility is 0.5u(10,000)+0,5u(100). Because u(x)=x^1/2 we get u(10,000)=100 and u(100)=10. Thus, the expected utility is 55.
• If you receive 4,900 Dollars with probability 1, then the expected utility is u(4,900)=70.
• The expected utility of receiving x and y with probability 0.5 each is given by 0.5x^1/2+0.5y^1/2. The certainty equivalent is therefore a payment z with u(z)=0.5x^1/2+0.5y^1/2. Thus, z^1/2=0.5x^1/2+0.5y^1/2, which implies that the certainity equivalent is (0.5x^1/2+0.5y^1/2)².
• If x=10,000 and y=10, then we get a certainity equivalent of 55²=3,025. Note that the expected value of the lottery is 5,050. Thus, in order for the agent to be willing to choose the lottery of the certain payment, the lottery must have a much higher expected payoff than then the certain payment.

Question 6: Her expected utility is given by 0.25u(1600)+0.70u(0)=10, since u(1600)=40 and u(0)=0. If she gets x Dollars with probability 1 her utility is u(x)=x^1/2. In order for her to be willing to sell, we must have u(x)>=10. Thus, x^1/2>=10 which implies x>=100. Thus, she must receive at least 100 Dollars.

To the title page