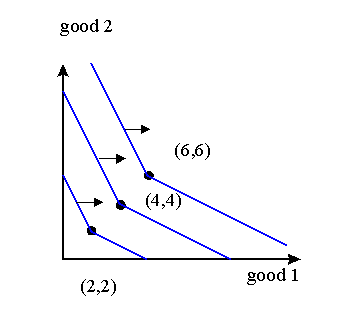
Question 1: In order to find indifference curves we start from a particular consumption bundle, say (2,2). We want to find exchanges Dx₂/Dx₁ that lead to other consumption bundles on the same indifference curve.

Note that the exchange ratio is Dx₂/Dx₁=-1/2 if x₁>=x₂, and Dx₂/Dx₁=-2 if x₂>=x₁. Thus, the indifference curves have a kink at x₁=x₂.

Question 2:

• Note that u₁(x₁,x₂)=1 and u₂(x₁,x₂)=4, because of additivity. Thus, since MRS(x)=-u₁/u₂, we get MRS=-1/4.
• u₁(x₁,x₂) =2x₁ and u₂(x₁,x₂)=1. Thus, the MRS is given by MRS(x)=-2x₁.
• u₁(x₁,x₂) = 1 and u₂(x₁,x₂) = (1/x₂²), because of additivity. Thus, MRS(x)=-1/(1/x₂²)=-x₂²
• u₁(x₁,x₂) = (1/2)x₁^-1/2=1/(2x₁^1/2), and u₂(x₁,x₂) = (1/2)x₂^-1/2 = 1/(2x₂^1/2) Thus, the MRS is given by MRS(x)=-x₂^1/2/x₁^1/2.

Question 3:

• At (8,2) it follows that 2x₁+x₂=18 and x₁+2x₂=12. Thus, his utility is 12, the smaller of the two numbers 18 and 12.
• When graphing the indifference curve for which u(x₁,x₂)=12, first graph the two lines 2x₁+x₂=12 and x₁+2x₂=12. Clearly, any consumption bundle which is to the right of both lines in you graph has a utility of at least 12. The set of all such consumption bundles is the at least as good set (blue in the graph). The lower boundary of the set is the indifference curve. It is the collection of consumption bundles which are on one of the two lines but to the right of the other one. In order to get the indifference curve for the utility level 6, we proceed as above (substituting the number 12 by the number 6).
  

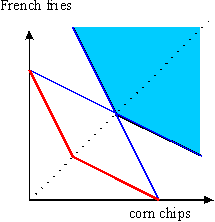
• At (5,2) we get 2x₁+x₂=12 and x₁+2x₂=7. Thus, x₁+2x₂=7 describes the indifference curve at (5,2). This is a straight line with slope -1/2, i.e., the MRS= Dx_f/Dx_c=-1/2 where x_f is the amount of fries and x_c the amount of chips. If x_f=1 then x_c=-2. Therefore he would be willing to trade 2 units of corn chips for one unit of fries.

Question 4: The indifference curves are L shaped (perfect complements) as in Figure 3.4 or 5.6 in the textbook. The only difference is that the "kink" of each indifference curve occurs at consumption bundles (x₁,x₂) for which x₁=3x₂ (e.g., (3,1), (6,2), etc).

The utility of (5,5) is 5. The utility of (5.01,4) is 5.01. Thus, the consumer would trade.

The utility of (4.99,6) is 4.99. Thus, the consumer would not trade.

Question 5: A utility function is u(x₁,x₂) = min{x₁,x₂} or any monotonic transformation of it. E.g., u(x₁,x₂) = min{x₁,x₂}² or u(x₁,x₂) =100 min{x₁,x₂}²+10, etc.,

Question 6:

• Yes
• No
• Yes
• Yes
• Yes
• No
• Yes

Question 7: Martha has a Cobb-Douglas utility function which is a monotonic transformation of u(x₁,x₂) = x₁x₂. The graph of the indifference curves are indicated below on the left (they should look approximately like that in Figure 4.3 in the textbook)

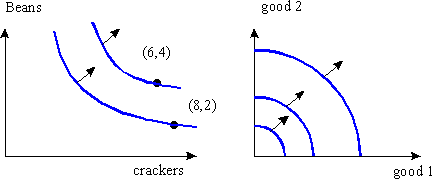
Bertha's preferences are exactly the same. They are just a monotonic transformation of Bertha's. Thus, you get the same picture. Moreover, both preferences are convex.

Question 8: The indifference curves are quarter circles centered at (0,0) as indicated in the graph above (on the right). The preferences are not convex.

To the title page