Question 1:

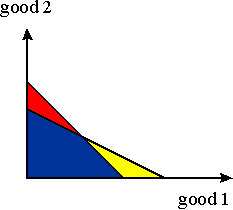
• The budget constraint is given by 10x₁+20x₂=<200.
• Thus, the budget line is given by 10x₁+20x₂=200. The intercepts are (20,0) and (0,10). The slope is -p₁/p₂=-10/20=-0.5.
• The budget set is the area underneath the budget line (yellow + blue area).
• The new budget line is 20x₁+20x₂=300.
• The intercepts are (15,0) and (0,15). The slope is -p₁/p₂=-1
• The new budget set consists of the red + blue area.

Question 2: The budget line is given by x₁+2x₂+10x₃=50. Thus, (x₁+Dx₁) + 2(x₂+Dx₂) + 10(x₃ + Dx₃) = 50. This is equivalent to

Because x₁+2x₂+10x₃=50 we can conclude that

• Now assume that Dx₁=0. Then, 2Dx₂+10Dx₃ = 0, and hence Dx₂/Dx₁=-5.
• Now Dx₂=0. Then, Dx₁+10Dx₃ = 0, and hence Dx₁/Dx₃=-10.
• We have shown that Dx₁/Dx₃=-10. Since Dx₃=-2 we therefore get Dx₁=20. Thus, consumption of good 1 can be increased by 20 units.

Question 3:

• 12x₁+5x₂=200, as the quantity tax of 2 Dollars increases the price of good 1 by 2 Dollars. The intercepts are (200/12,0), (0,40). The slope is -12/5.
• 12x₁+5x₂=200. The value tax of 20% Dollars increases the price of good 1 by 20% Dollars. This gives the same answer as above,
• 9x₁+5x₂=200, as the quantity subsidy of 1 Dollars decreases the price of good 1 by 1 Dollar. The intercepts are (200/9,0), (0,40). The slope is -9/5.
• 10x₁+5x₂=240. The lump sum subsidy of 2 Dollars increases income to 240 Dollars. The intercepts are (24,0), (0,48). The slope is -2.

Question 4:

• The vertical intercept is (0,200), because the consumer has 200 Dollars for consumption of the composite good 2 since the consumption of good one is 0.
• Recall that Dx₂/Dx₁=-p₁/p₂. Starting from the vertical intercept, increase x₁ by 10. Thus, Dx₁=10. The price ratio is -p₁/p₂=-10. Thus, Dx₂=-100, i.e., if starting from the vertical intercept we increase x₁ by 10 units we must decrease x₂ by 100 units. Thus, we get (10,100).

  The following is an alternatively argument. If we buy 10 units of good 1 we spend 100 Dollars. This reduces the amount of the composite good from 200 to 100.

• Now we want to reduce x₂ to 0 (starting from (10,100)). Thus, Dx₂=-100 Therefore, -100/Dx₁=-p₁/p₂=-15. Therefore, Dx₁=100/15=20/3=6.667.
• We have already determined the slopes above. Specifically, the slopes are -10 and -15, respectively.
• For x=<10 the prices are 10 and 1, respectively. Thus, the budget line must be of the form 10x₁+x₂=k, where we must determine k. Recall that (0,200) is on the budget line. Thus, k=200 and we get 10x₁+x₂=200.
• For x>=10 the prices are 15 and 1, respectively. Thus, the budget line must be of the form 15x₁+x₂=k, where we must again determine k. Recall that (10,100) is on the budget line. Thus, 150+100=250=k. Therefore, for x>=10, the budget line is given by 15x₁+x₂=250.

Question 5: The equation of the budget line is 2P+4M+6J=360.

If potatoes should become the numeraire then we must normalize prices such that the price of one sack of potatoes becomes 1. In other words, divide both sides of the equation by 2. This yields P+2M+3J=180.

Thus, the new price of meatballs is 2, the new price of jam is 3 and the new income he would need is 180.

As mentioned above, the new budget line equation is P+2M+3J=180. This describes exactly the same budget line as 2P+4M+6J=360.

Question 6:

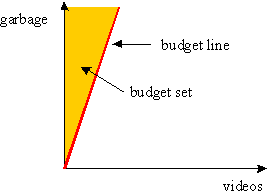
(a) Since he has no other sources of income, his consumption of video casettes is 0.

(b) He receives 30 Dollars for the garbage. Thus, he can purchase 5 videos.

(c) The budget line equation is 6C-2G=0 or 6C=2G.

Question 7: Note that since both blue and red money must be used, a consumption bundle is affordable if and only if it is fulfills both the red and the blue budget constraint.

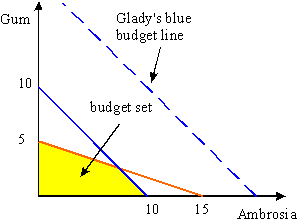
Note that Glady's blue budget line is strictly to the right of the red one. Thus, both constraints are fulfilled if and only if the red one holds.

If a consumer can choose to use either blue or red money then the resulting budget set is the set of all consumption bundles which fulfill either the blue or the red budget constraint.

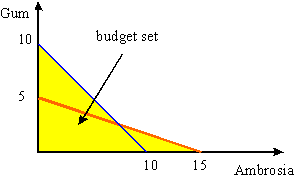
An example would be a time constraint people face in addition to a standard budget constraint.

To the title page