Question 1:

• f(x)=x²/(1+4x). Use the quotient rule. Thus, g(x)=x², h(x)=1+4x, g '(x)=2x, and h '(x)=4. This implies
  f '(x)=[2x(1+4x)-4x²] / (1+4x)² = [2x+4x²] / (1+4x)².

• f(x)=ln(x+20). Use the chain rule. g(x)=ln (x) and h(x)=x+20. Since h '(x)=1 because of additivity, it follows that f '(x)=1/(x+20).
• f(x)=ln(x+a). Same as above. Only difference h(x)=x+a. Again, additivity, implies h '(x)=1. Thus, f '(x)=1/(x+a).
• f(x)=(x²+5)^1/2. Again use the chain rule, choosing g(x)=x^1/2 and h(x)=4+x⁴. The derivatives are g '(x)=(1/2)x^-1/2 and h '(x)=4x³ (because of additivity the number 4 drops out). Thus, f '(x)=(1/2)(4+x⁴)^-1/24x³ = 2x³ / (4+x⁴)^1/2.
• f(x)=(a+x⁴)^1/2. The only difference to the previous question is that now h(x)=a+x⁴. Again because of additivity a drops out, since it is a fixed number. The answer is therefore f '(x) = 2x³ / (a+x⁴)^1/2.
• f(x)=3x²+6x⁴. Because of additivity f '(x) is the sum of the derivative of 3x² and of 6x⁴. Thus, f '(x)=6x+24x³.
• Because of linearity the derivative of ax² is 2ax and of bx⁴ is 4bx³. Thus, f '(x)=2ax+4bx³.

• f(x,y)=xy³. Derivative with respect to x: Now y (and thus y³) is treated like a constant. Thus, linearity implies f_x=y³. Similarly f_y=3xy².
• f(x,y)=x+20y. To take the derivative with respect to x, y is treated like a constant. Thus, we have essentially an expression of the form x+a, where a is fixed. Thus, additivity implies f_x=1. Similarly, it follows that f_y=20.
• Same idea as above, i.e., one of the summands is a constant when taking the partial derivative. Thus f_x=10/x and f_y=1/y.
• Use the quotient rule. g(x,y)=x+2y, h(x,y)=y. The partials are g_x=1, g_y=2, h_y=1 and h_x=0. Thus, f_x=1/y and f_y = (2y-x+2y)/y²= -x/y².
• f(x,y)=2x²+y. Again, additivity implies f_x=4x and f_y=1.
• f(x,y)=ax²+by. Now additivity and the rule of multiplication with scalars implies f_x=2ax and f_y=b.

• x²y=20 immediately implies y=20/x².
• The slope is given by the derivative of 20/x² at x=2.
  The derivative of 20/x² is -40/x³. Thus, if x=2 we get -40/8=-5.
• The value of y is 5 at x=2.
  

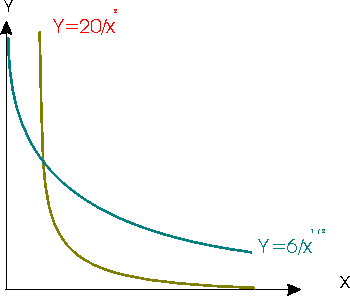
• y²=36/x. Thus, y=6/x^1/2 (recall that x^1/2 is the square root of x).
• The slope is given by the derivative of 6/x^1/2 at x=4.
  The derivative is -3/x^-3/2. Thus, if x=4 we get -3/8.
• y=3 at x=4.

To the title page