Econ 302: Solutions for the Questions about Preferences and Utility Functions
Question 1:
- true
- true
- false
- false
- false
Question 2: The equation of the three indifference curves are given by
- x1-4x2=-6
- x1-4x2=-16
- x1-4x2=4
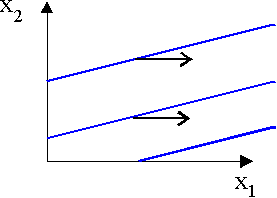 Note that the values on the right hand side are the utilities of
(2,2), (0,4), and (4,0) and that the equation just specifies that all
consumption bundles must have the same utilities.
These are equations of straight lines with slope 1/4. See the graph.
Note that the arrows point to the right.
Note that the values on the right hand side are the utilities of
(2,2), (0,4), and (4,0) and that the equation just specifies that all
consumption bundles must have the same utilities.
These are equations of straight lines with slope 1/4. See the graph.
Note that the arrows point to the right.
Question 3:
- no (increase good 2)
- yes
- yes (note that if you increase good 2, 1/x2 decreases. However, this means that 1/x2 increases).
- yes.
Question 4:
- Note that u1(x1,x2)=1 and u2(x1,x2)=3, because of additivity. Thus, since MRS(x)=-u1/u2, we get MRS=-1/3.
- Now u1(x1,x2)=3 and u2(x1,x2)=-1, again because of additivity. Thus, we get MRS=3. Note that the MRS is positive, i.e., the indifference curves have a positive slope. This is the case because good 2 is undesirable.
- u1(x1,x2) =(1/4)x1-3/4, and u2(x1,x2)=2. Thus, the MRS is given by MRS(x)=-(1/8)x1-3/4.
- u1(x1,x2) =(1/4)x1-3/4,
and u2(x1,x2) =(1/4)x2-3/4.
Thus,
MRS(x)= - (1/4)x1-3/4 = - x23/4 (1/4)x2-3/4 x13/4 - u1(x1,x2) = 1 and u2(x1,x2) = -2/x2-3. Thus, MRS(x)=-1/(-2/x2-3) =(1/2)x23. Again, the MRS is positive because one of the goods (good 2) is undesirable.
- u1(x1,x2) = 10 and u2(x1,x2) = 1. Thus, MRS(x)=-10.
- u1(x1,x2) = 4 and u2(x1,x2) = 5. Thus, MRS(x)=-4/5.