logo

Applied Econometrics 
Econ 508 - Fall 2014

Professor: Roger Koenker

TA: Nicolas Bottan

Welcome to e-Tutorial, your on-line help to Econ508. This issue provides an introduction on how to do the piratical works about the Delta-method and bootstrap in R. Hope this will be helpful for your further understanding of Prof. Koenker’s Lecture 5.1

Data Set

The data set used in this tutorial was borrowed from Johnston and DiNardo’s Econometric Methods (1997, 4th ed), but slightly adjusted for your needs. It is called AUTO2. You can download the data by visiting the Econ 508 web site (Data). As you will see, this adapted data set contains five series.

    use AUTO2, clear
    describe
  obs:           128                          AUTO2 adapted from Johnston and DiNard
 vars:             5                          11 Sep 2002 12:22
 size:         2,560                          
------------------------------------------------------------------------------------
              storage  display     value
variable name   type   format      label      variable label
------------------------------------------------------------------------------------
quarter         float  %9.0g                  Quarter of the observation
gas             float  %9.0g                  Log of per capita real expenditure on 
price           float  %9.0g                  Log of the real price of gasoline and 
income          float  %9.0g                  Log of per capita real disposable inco
miles           float  %9.0g                  Log of miles per gallon
------------------------------------------------------------------------------------
Sorted by:

As we did before we need to transform the data in “time series” first:

    gen t = _n    
    label variable t "Integer time period"
    tsset t
         time variable:  t, 1 to 128
                delta:  1 unit

Running a Dynamic Model with Quadratic and Multiplicative Terms

In the problem set 2, question 4, you are asked to run a linear regression model with non-linear transformation of variables. Suppose for a moment that you have in your hands a data set like the one used here (auto2.dta), and would like to estimate an equation similar to the problem set:

\[gas_{t} = b_{0} + b_{1} income_{t} + b_{2} price_{t} + b_{3} price_{t} ^2 + b_{4} (price_{t}*income_{t}) + u_{t}\]

first you need first to generate the quadratic and other terms as follows:

    gen price2= price^2 
    gen priceinc= price*income

then regress:

    regress gas income price price2 priceinc
      Source |       SS       df       MS              Number of obs =     128
-------------+------------------------------           F(  4,   123) =  117.59
       Model |  1.45421455     4  .363553638           Prob > F      =  0.0000
    Residual |   .38027632   123  .003091677           R-squared     =  0.7927
-------------+------------------------------           Adj R-squared =  0.7860
       Total |  1.83449087   127   .01444481           Root MSE      =   .0556

------------------------------------------------------------------------------
         gas |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
      income |  -6.109449   2.750048    -2.22   0.028      -11.553   -.6658978
       price |   3.090076   2.894747     1.07   0.288    -2.639898     8.82005
      price2 |   .2839261   .1693137     1.68   0.096      -.05122    .6190723
    priceinc |   1.454257   .5879186     2.47   0.015      .290508    2.618006
       _cons |  -25.52231    11.8968    -2.15   0.034     -49.0713   -1.973312
------------------------------------------------------------------------------

Now, suppose you are asked to calculate the price elasticity of demand at different points of the sample. To do that you will need to:

  1. Obtain the coefficients of regression:
    matrix B=get(_b) 
    matrix list B
B[1,5]
        income       price      price2    priceinc       _cons
y1  -6.1094494   3.0900762   .28392614   1.4542568  -25.522308
  1. Extract the coefficients to scalars:
    scalar b1=_coef[income] 
    scalar b2=_coef[price] 
    scalar b3=_coef[price2] 
    scalar b4=_coef[priceinc] 
    scalar b0=_coef[_cons]  
    scalar list b1 b2 b3 b4 b0
Or another way to do it: scalar b1=B[1,1] or scalar b1=_b[income]
 iii.  Calculate the elasticity at different:
    gen elastpt=b2+2*b3*price+b4*income 
    summarize elastpt, detail
                           elastpt
-------------------------------------------------------------
      Percentiles      Smallest
 1%    -.7897052      -.8065645
 5%    -.7665387      -.7897052
10%    -.7234885      -.7795596       Obs                 128
25%    -.4959842      -.7698234       Sum of Wgt.         128

50%    -.2754352                      Mean          -.3273864
                        Largest       Std. Dev.      .2598182
75%    -.0774807       .0347935
90%    -.0073602       .0391868       Variance       .0675055
95%     .0219321       .0460309       Skewness      -.2600589
99%     .0460309       .0555678       Kurtosis       1.835793
 iv. Ok. You've just created your elasticity series. Now you can study it at different points of the sample, plot it against year  (check for inter-temporal structural breaks), against price, and against income. 
scatter elastpt  quarter, xlabel(1960.1 (5) 1990.1) t1title(Price Elasticity vs. Time) 


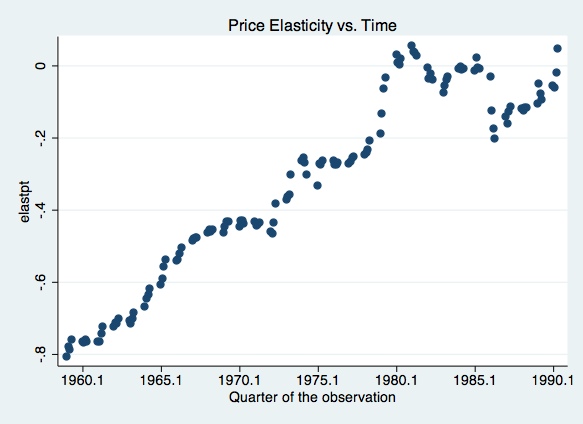
    scatter elastpt gas, t1title(Price Elasticity vs. Gas Expenditure)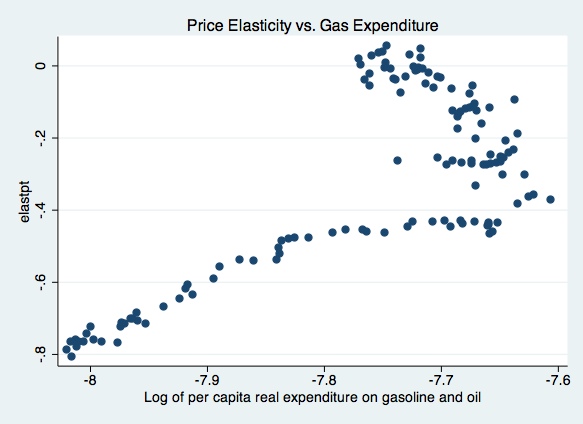



    scatter elastpt price, t1title(Price Elasticity vs. Price)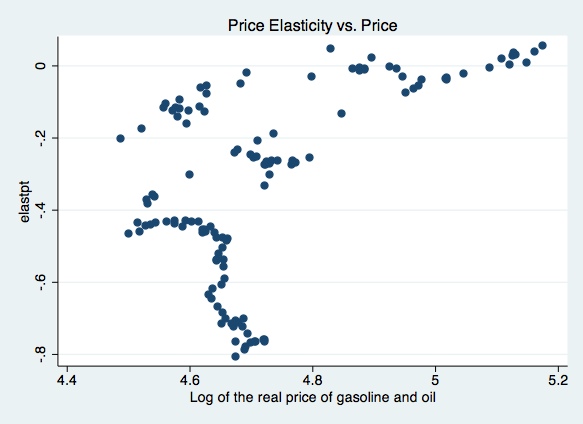



Tip for problem set 2, question 5.

For this question you should:

  1. Interpret the implications of the model.

  2. Calculate the price such that \([b_{2}+2*b_{3}*price+b_{4}*income] = -1 \) Given the formula of elasticity, and assuming \(income=x_{0}\), just find the optimal price. Call it \(p^{*}\).

  3. Examine the partial residual plots

  4. Finally, in the last part of the question 5 you are asked to estimate model 2 and to compute the revenue maximizing price level assuming \(income=\$30.000\) per year. This is a straightforward computation. The interesting part come with the application of the delta method and the bootstrap to achieve reasonable confidence intervals for the optimal price.

Delta-method and Bootstrap

Note that we obtained point estimates. To compute confidence intervals, you will need the Delta-method and/or Bootstrap. In the problem set you are asked to assume that \(income=\$30.000\) per year. For this e-ta, we will assume \(income=log(15)=2.708050\) approximately

Delta-method

For the problem set you are expected to sketch the Delta-method and calculate the derivatives by hand along with the computational routine below.

  1. Start running the full model again:
   regress gas income price price2 priceinc 
       Source |       SS       df       MS              Number of obs =     128
-------------+------------------------------           F(  4,   123) =  117.59
       Model |  1.45421455     4  .363553638           Prob > F      =  0.0000
    Residual |   .38027632   123  .003091677           R-squared     =  0.7927
-------------+------------------------------           Adj R-squared =  0.7860
       Total |  1.83449087   127   .01444481           Root MSE      =   .0556

------------------------------------------------------------------------------
         gas |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
      income |  -6.109449   2.750048    -2.22   0.028      -11.553   -.6658978
       price |   3.090076   2.894747     1.07   0.288    -2.639898     8.82005
      price2 |   .2839261   .1693137     1.68   0.096      -.05122    .6190723
    priceinc |   1.454257   .5879186     2.47   0.015      .290508    2.618006
       _cons |  -25.52231    11.8968    -2.15   0.034     -49.0713   -1.973312
------------------------------------------------------------------------------
  1. Recall that you have stored those coefficients under the names b0, b1, b2 , b3, b4. Now you need to get the covariance matrix V of them:
    matrix V=get(VCE) 
    matrix list V
 symmetric V[5,5]
              income       price      price2    priceinc       _cons
  income   7.5627648
   price  -6.5629988   8.3795596
  price2  -.00833388  -.27004512   .02866714
priceinc  -1.6166822    1.405926   .00149168   .34564825
   _cons    30.88608  -33.229023   .62976256  -6.6089597   141.53396
  1. Next you need to input pstar:
  scalar pstar = -(1+b2+b4*ln(15))/(2*b3) 
  scalar list pstar
  pstar = -14.137967
  1. And then you need to obtain the gradient vector with the partial derivatives of pstar (optimal price) with respect to each regressor, obeying the order of the covariance matrix:

\[G'= (\frac{\partial{p^{*}}}{\partial{cons}}, \frac{\partial{p^{*}}}{\partial{income}}, \frac{\partial{p^{*}}}{\partial{price}}, \frac{\partial{p^{*}}}{\partial{price2}}, \frac{\partial{p^{*}}}{\partial{price\_income}}) \]

In Stata the vector will be as follows (note that the backslashes separate each row of the vector):

  matrix G=( 0  \  -1/(2*b3)  \  (1+b2+b4*ln(15))/(2*b3*b3)  \  -ln(15)/(2*b3)  \  0) 
  matrix list G
 G[5,1] 
            c1 
r1           0 
r2  -1.7610213 
r3   49.794522 
r4  -4.7689342 
r5           0
  1. The next step is to obtain the estimated variance of the optimal price, \(G'VG\):
   matrix GVG=G'*V*G 
   matrix list
symmetric GVG[1,1]
           c1
c1  175.19377
  1. Then you can obtain the standard error by taking the square root of this scalar value:
   scalar sepstar=sqrt(el(GVG,1,1)) 
   scalar list sepstar
   sepstar =  13.236079

That’s it. The variable sepstar is the standard error of pstar.

  1. The last step is to construct your confidence interval, and put the variables in levels, as follows:
   scalar CIupper=pstar + 1.96*sepstar 
   scalar CIlower=pstar - 1.96*sepstar 
   scalar list CIlower pstar CIupper 
   CIlower =  -40.08068
     pstar = -14.137967
   CIupper =  11.804747

This will give you the confidence interval of the optimal price level. Observe that the results you obtained are for prices in logs. You can try to get the respective results in levels as well, but it is worth to think about whether you can do that directly or you need some additional step because of the non-linearity of the point estimate.

Bootstrap

You are expected to explain the various Bootstrap techniques in words (as if you are explaining for a non-econometrician), along with the complete understanding of the results provided by STATA.

In STATA, you can calculate parametric (Normal), percentiled, and bias corrected bootstrapped confidence intervals for the optimal price as follows:

 bs pr=(-1*(1+_b[price]+_b[priceinc]*ln(15))/(2*_b[price2])), reps(1000): 
    reg gas income price price2 priceinc
Bootstrap replications (1000)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5 
..................................................    50
..................................................   100
..................................................   150
..................................................   200
..................................................   250
..................................................   300
..................................................   350
..................................................   400
..................................................   450
..................................................   500
..................................................   550
..................................................   600
..................................................   650
..................................................   700
..................................................   750
..................................................   800
..................................................   850
..................................................   900
..................................................   950
..................................................  1000

Linear regression                               Number of obs      =       128
                                                Replications       =      1000

      command:  regress gas income price price2 priceinc
           pr:  -1*(1+_b[price]+_b[priceinc]*ln(15))/(2*_b[price2])

------------------------------------------------------------------------------
             |   Observed   Bootstrap                         Normal-based
             |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
          pr |  -14.13797   270.9505    -0.05   0.958    -545.1913    516.9153
------------------------------------------------------------------------------
In the command above, you use set seed 1 to assure reproducibility of your results. It means that, instead of generating a different initial random number every time you run the bootstrap, STATA will use the same seed, i.e., same initial random number (equals 1 in this case), for the iteration process.  The first expression in quotation marks is the estimator, while the second quoted expression is the estimate you are interested.  reps (10000) means that STATA will repeat the process 10000 times, to give  you the confidence interval.

Recall the generated statistic is in log form. A good question is whether you should present your Delta-method and Bootstrap confidence interval in logs or in levels... Think about it.

Appendix A: Partial Residual Plot Revisited

It is important to mention that all results presented here are based on a different data set (auto2.dta) than the data set used on the problem set 2 (gasnew.dat):

  1. Use the partial residual plot to check on the effect of the quadratic term. To obtain the partial residual plot with respect to the quadratic term you should :

1.1) Estimate model (2) without the regressor price2, and call this model (2.1)

    quietly: regress gas income price priceinc

1.2) Obtain the residuals of the model (2.1):

    predict gasres, resid

1.3) Estimate model (2) using price2 instead of gas as the dependent variable; call it model (2.2):

    quietly: regress price2 income price priceinc

1.4) Obtain the residuals of the model (2.2):

    predict pric2res, resid

1.5) Run the Gauss-Frisch-Waugh “regression”, and check if the slope coefficient is the same as in the original model (2):

    regress gasres pric2res
      Source |       SS       df       MS              Number of obs =     128
-------------+------------------------------           F(  1,   126) =    2.88
       Model |  .008694019     1  .008694019           Prob > F      =  0.0921
    Residual |  .380276321   126  .003018066           R-squared     =  0.0224
-------------+------------------------------           Adj R-squared =  0.0146
       Total |   .38897034   127  .003062759           Root MSE      =  .05494

------------------------------------------------------------------------------
      gasres |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
    pric2res |   .2839261   .1672859     1.70   0.092    -.0471278    .6149801
       _cons |   2.57e-10   .0048558     0.00   1.000    -.0096095    .0096095
------------------------------------------------------------------------------

1.6) Plot the the partial residuals, with a fitting line of predicted values

 twoway (scatter gasres pric2res) (lfit gasres pric2res), title(Partial Residuals)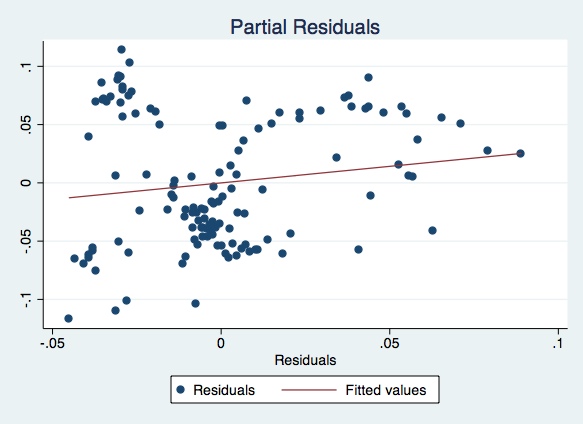


  1. Check whether there is a linear relationship between the residuals of the model (2.1) and the residuals of model (2.2). Draw your conclusion from what you see in the graph, and try to justify your answer in the light of basic assumptions of linear regression.

  1. Please send comments to bottan2@illinois.edu or srmntbr2@illinois.edu?

<!-- dynamically load mathjax for compatibility with --self-contained -->